Hasil pengukuran yang kita peroleh disebut dengan data mentah.
Besarnya hasil pengukuran yang kita peroleh biasanya bervariasi. Apabila
kita perhatikan data mentah tersebut, sangatlah sulit bagi kita untuk
menarik kesimpulan yang berarti. Untuk memperoleh gambaran yang baik
mengenai data tersebut, data mentah tersebut perlu di olah terlebih
dahulu.
Pada saat kita dihadapkan pada sekumpulan data yang banyak, seringkali membantu untuk mengatur dan merangkum data tersebut dengan membuat tabel yang berisi daftar nilai data yang mungkin berbeda (baik secara individu atau berdasarkan pengelompokkan) bersama dengan frekuensi yang sesuai, yang mewakili berapa kali nilai-nilai tersebut terjadi. Daftar sebaran nilai data tersebut dinamakan dengan Daftar Frekuensi atau Sebaran Frekuensi (Distribusi Frekuensi).
Dengan demikian, distribusi frekuensi adalah daftar nilai data (bisa nilai individual atau nilai data yang sudah dikelompokkan ke dalam selang interval tertentu) yang disertai dengan nilai frekuensi yang sesuai.
Pengelompokkan data ke dalam beberapa kelas dimaksudkan agar ciri-ciri penting data tersebut dapat segera terlihat. Daftar frekuensi ini akan memberikan gambaran yang khas tentang bagaimana keragaman data. Sifat keragaman data sangat penting untuk diketahui, karena dalam pengujian-pengujian statistik selanjutnya kita harus selalu memperhatikan sifat dari keragaman data. Tanpa memperhatikan sifat keragaman data, penarikan suatu kesimpulan pada umumnya tidaklah sah.
Sebagai contoh, perhatikan contoh data pada Tabel 1. Tabel tersebut adalah daftar nilai ujian Matakuliah Statistik dari 80 Mahasiswa (Sudjana, 19xx).
Tabel 1. Daftar Nilai Ujian Matakuliah Statistik
Sangatlah sulit untuk menarik suatu kesimpulan dari daftar data
tersebut. Secara sepintas, kita belum bisa menentukan berapa nilai ujian
terkecil atau terbesar. Demikian pula, kita belum bisa mengetahui
dengan tepat, berapa nilai ujian yang paling banyak atau berapa banyak
mahasiswa yang mendapatkan nilai tertentu. Dengan demikian, kita harus
mengolah data tersebut terlebih dulu agar dapat memberikan gambaran atau
keterangan yang lebih baik.
Bandingkan dengan tabel yang sudah disusun dalam bentuk daftar frekuensi (Tabel 2a dan Tabel 2b). Tabel 2a merupakan daftar frekuensi dari data tunggal dan Tabel 2b merupakan daftar frekuensi yang disusun dari data yang sudah di kelompokkan pada kelas yang sesuai dengan selangnya. Kita bisa memperoleh beberapa informasi atau karakteristik dari data nilai ujian mahasiswa.
Tabel 2a.
Pada Tabel 2a, kita bisa mengetahui bahwa ada 80 mahasiswa yang
mengikuti ujian, nilai ujian terkecil adalah 35 dan tertinggi adalah 99.
Nilai 70 merupakan nilai yang paling banyak diperoleh oleh mahasiswa,
yaitu ada 4 orang, atau kita juga bisa mengatakan ada 4 mahasiswa yang
memperoleh nilai 70, tidak ada satu pun mahasiswa yang mendapatkan nilai
36, atau hanya satu orang mahasiswa yang mendapatkan nilai 35.
Tabel 2b.
Tabel 2b merupakan daftar frekuensi dari data yang sudah
dikelompokkan. Daftar ini merupakan daftar frekuensi yang sering
digunakan. Kita sering kali mengelompokkan data contoh ke dalam
selang-selang tertentu agar memperoleh gambaran yang lebih baik mengenai
karakteristik dari data. Dari daftar tersebut, kita bisa mengetahui
bahwa mahasiswa yang mengikuti ujian ada 80, selang kelas nilai yang
paling banyak diperoleh oleh mahasiswa adalah sekitar 71 sampai 80,
yaitu ada 24 orang, dan seterusnya. Hanya saja perlu diingat bahwa
dengan cara ini kita bisa kehilangan identitas dari data aslinya.
Sebagai contoh, kita bisa mengetahui bahwa ada 2 orang yang mendapatkan
nilai antara 31 sampai 40. Meskipun demikian, kita tidak akan tahu
dengan persis, berapa nilai sebenarnya dari 2 orang mahasiswa tersebut,
apakah 31 apakah 32 atau 36 dst.
Ada beberapa istilah yang harus dipahami terlebih dahulu dalam menyusun daftar frekuensi.
Tabel 3.
Range : Selisih antara nilai tertinggi dan terendah. Pada contoh ujian di atas, Range = 99 – 35 = 64
Batas bawah kelas: Nilai terkecil yang berada pada setiap kelas. (Contoh: Pada Tabel 3 di atas, batas bawah kelasnya adalah 31, 41, 51, 61, …, 91)
Batas atas kelas: Nilai terbesar yang berada pada setiap kelas. (Contoh: Pada Tabel 3 di atas, batas bawah kelasnya adalah 40, 50, 60, …, 100)
Batas kelas (Class boundary): Nilai yang digunakan untuk memisahkan antar kelas, tapi tanpa adanya jarak antara batas atas kelas dengan batas bawah kelas berikutnya. Contoh: Pada kelas ke-1, batas kelas terkecilnya yaitu 30.5 dan terbesar 40.5. Pada kelas ke-2, batas kelasnya yaitu 40.5 dan 50.5. Nilai pada batas atas kelas ke-1 (40.5) sama dengan dan merupakan nilai batas bawah bagi kelas ke-2 (40.5). Batas kelas selalu dinyatakan dengan jumlah digit satu desimal lebih banyak daripada data pengamatan asalnya. Hal ini dilakukan untuk menjamin tidak ada nilai pengamatan yang jatuh tepat pada batas kelasnya, sehingga menghindarkan keraguan pada kelas mana data tersebut harus ditempatkan. Contoh: bila batas kelas di buat seperti ini:
Kelas ke-1 : 30 – 40
Kelas ke-2 : 40 – 50
:
dst.
Apabila ada nilai ujian dengan angka 40, apakah harus ditempatkan pada kelas-1 ataukah kelas ke-2?
Panjang/lebar kelas (selang kelas): Selisih antara dua nilai batas bawah kelas yang berurutan atau selisih antara dua nilai batas atas kelas yang berurutan atau selisih antara nilai terbesar dan terkecil batas kelas bagi kelas yang bersangkutan. Biasanya lebar kelas tersebut memiliki lebar yang sama. Contoh:
lebar kelas = 41 – 31 = 10 (selisih antara 2 batas bawah kelas yang berurutan) atau
lebar kelas = 50 – 40 = 10 (selisih antara 2 batas atas kelas yang berurutan) atau
lebar kelas = 40.5 – 30.5 = 10. (selisih antara nilai terbesar dan terkecil batas kelas pada kelas ke-1)
Nilai tengah kelas: Nilai kelas merupakan nilai tengah dari kelas yang bersangkutan yang diperoleh dengan formula berikut: ½ (batas atas kelas+batas bawah kelas). Nilai ini yang dijadikan pewakil dari selang kelas tertentu untuk perhitungan analisis statistik selanjutnya. Contoh: Nilai kelas ke-1 adalah ½(31+40) = 35.5
Banyak kelas: Sudah jelas! Pada tabel ada 7 kelas.
Frekuensi kelas: Banyaknya kejadian (nilai) yang muncul pada selang kelas tertentu. Contoh, pada kelas ke-1, frekuensinya = 2. Nilai frekuensi = 2 karena pada selang antara 30.5 – 40.5, hanya ada 2 angka yang muncul, yaitu nilai ujian 31 dan 38.
Langkah-langkah dalam menyusun tabel distribusi frekuensi:
Contoh:
Kita gunakan prosedur di atas untuk menyusun tabel distribusi frekuensi nilai ujian mahasiswa (Tabel 1).
Frekuensi relatif =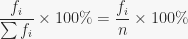
Contoh: frekuensi relatif kelas ke-1:
fi = 2; n = 80
Frekuensi relatif = 2/80 x 100% = 2.5%
Perhatikan bahwa kolom frekuensi selain label headernya diganti dengan frekuensi kumulatif kurang dari, batas-batas kelas diganti dengan “kurang dari” ekspresi yang menggambarkan kisaran nilai-nilai baru.
atau kadang disusun dalam bentuk seperti ini:
Variasi lain adalah Frekuensi kumulatif lebih dari. Prinsipnya hampir sama dengan prosedur di atas.



Pada saat kita dihadapkan pada sekumpulan data yang banyak, seringkali membantu untuk mengatur dan merangkum data tersebut dengan membuat tabel yang berisi daftar nilai data yang mungkin berbeda (baik secara individu atau berdasarkan pengelompokkan) bersama dengan frekuensi yang sesuai, yang mewakili berapa kali nilai-nilai tersebut terjadi. Daftar sebaran nilai data tersebut dinamakan dengan Daftar Frekuensi atau Sebaran Frekuensi (Distribusi Frekuensi).
Dengan demikian, distribusi frekuensi adalah daftar nilai data (bisa nilai individual atau nilai data yang sudah dikelompokkan ke dalam selang interval tertentu) yang disertai dengan nilai frekuensi yang sesuai.
Pengelompokkan data ke dalam beberapa kelas dimaksudkan agar ciri-ciri penting data tersebut dapat segera terlihat. Daftar frekuensi ini akan memberikan gambaran yang khas tentang bagaimana keragaman data. Sifat keragaman data sangat penting untuk diketahui, karena dalam pengujian-pengujian statistik selanjutnya kita harus selalu memperhatikan sifat dari keragaman data. Tanpa memperhatikan sifat keragaman data, penarikan suatu kesimpulan pada umumnya tidaklah sah.
Sebagai contoh, perhatikan contoh data pada Tabel 1. Tabel tersebut adalah daftar nilai ujian Matakuliah Statistik dari 80 Mahasiswa (Sudjana, 19xx).
Tabel 1. Daftar Nilai Ujian Matakuliah Statistik
| 79 | 49 | 48 | 74 | 81 | 98 | 87 | 80 |
| 80 | 84 | 90 | 70 | 91 | 93 | 82 | 78 |
| 70 | 71 | 92 | 38 | 56 | 81 | 74 | 73 |
| 68 | 72 | 85 | 51 | 65 | 93 | 83 | 86 |
| 90 | 35 | 83 | 73 | 74 | 43 | 86 | 88 |
| 92 | 93 | 76 | 71 | 90 | 72 | 67 | 75 |
| 80 | 91 | 61 | 72 | 97 | 91 | 88 | 81 |
| 70 | 74 | 99 | 95 | 80 | 59 | 71 | 77 |
| 63 | 60 | 83 | 82 | 60 | 67 | 89 | 63 |
| 76 | 63 | 88 | 70 | 66 | 88 | 79 | 75 |
Bandingkan dengan tabel yang sudah disusun dalam bentuk daftar frekuensi (Tabel 2a dan Tabel 2b). Tabel 2a merupakan daftar frekuensi dari data tunggal dan Tabel 2b merupakan daftar frekuensi yang disusun dari data yang sudah di kelompokkan pada kelas yang sesuai dengan selangnya. Kita bisa memperoleh beberapa informasi atau karakteristik dari data nilai ujian mahasiswa.
Tabel 2a.
| No | Nilai Ujian | Frekuensi |
| xi | fi | |
| 1 | 35 | 1 |
| 2 | 36 | 0 |
| 3 | 37 | 0 |
| 4 | 38 | 1 |
| : | : | : |
| 16 | 70 | 4 |
| 17 | 71 | 3 |
| : | : | 1 |
| 42 | 98 | 1 |
| 43 | 99 | 1 |
| Total | 80 |
Tabel 2b.
| Kelas ke- | Nilai Ujian | Frekuensi fi |
| 1 | 31 – 40 | 2 |
| 2 | 41 – 50 | 3 |
| 3 | 51 – 60 | 5 |
| 4 | 61 – 70 | 13 |
| 5 | 71 – 80 | 24 |
| 6 | 81 – 90 | 21 |
| 7 | 91 – 100 | 12 |
| Jumlah | 80 |
Ada beberapa istilah yang harus dipahami terlebih dahulu dalam menyusun daftar frekuensi.
Tabel 3.
| Kelas ke- | Selang Nilai Ujian |
Batas Kelas | Nilai Kelas (xi) |
Frekuensi (fi) |
| 1 | 31 – 40 | 30.5 – 40.5 | 35.5 | 2 |
| 2 | 41 – 50 | 40.5 – 50.5 | 45.5 | 3 |
| 3 | 51 – 60 | 50.5 – 60.5 | 55.5 | 5 |
| 4 | 61 – 70 | 60.5 – 70.5 | 65.5 | 13 |
| 5 | 71 – 80 | 70.5 – 80.5 | 75.5 | 24 |
| 6 | 81 – 90 | 80.5 – 90.5 | 85.5 | 21 |
| 7 | 91 – 100 | 90.5 – 100.5 | 95.5 | 12 |
| Jumlah | 80 |
Batas bawah kelas: Nilai terkecil yang berada pada setiap kelas. (Contoh: Pada Tabel 3 di atas, batas bawah kelasnya adalah 31, 41, 51, 61, …, 91)
Batas atas kelas: Nilai terbesar yang berada pada setiap kelas. (Contoh: Pada Tabel 3 di atas, batas bawah kelasnya adalah 40, 50, 60, …, 100)
Batas kelas (Class boundary): Nilai yang digunakan untuk memisahkan antar kelas, tapi tanpa adanya jarak antara batas atas kelas dengan batas bawah kelas berikutnya. Contoh: Pada kelas ke-1, batas kelas terkecilnya yaitu 30.5 dan terbesar 40.5. Pada kelas ke-2, batas kelasnya yaitu 40.5 dan 50.5. Nilai pada batas atas kelas ke-1 (40.5) sama dengan dan merupakan nilai batas bawah bagi kelas ke-2 (40.5). Batas kelas selalu dinyatakan dengan jumlah digit satu desimal lebih banyak daripada data pengamatan asalnya. Hal ini dilakukan untuk menjamin tidak ada nilai pengamatan yang jatuh tepat pada batas kelasnya, sehingga menghindarkan keraguan pada kelas mana data tersebut harus ditempatkan. Contoh: bila batas kelas di buat seperti ini:
Kelas ke-1 : 30 – 40
Kelas ke-2 : 40 – 50
:
dst.
Apabila ada nilai ujian dengan angka 40, apakah harus ditempatkan pada kelas-1 ataukah kelas ke-2?
Panjang/lebar kelas (selang kelas): Selisih antara dua nilai batas bawah kelas yang berurutan atau selisih antara dua nilai batas atas kelas yang berurutan atau selisih antara nilai terbesar dan terkecil batas kelas bagi kelas yang bersangkutan. Biasanya lebar kelas tersebut memiliki lebar yang sama. Contoh:
lebar kelas = 41 – 31 = 10 (selisih antara 2 batas bawah kelas yang berurutan) atau
lebar kelas = 50 – 40 = 10 (selisih antara 2 batas atas kelas yang berurutan) atau
lebar kelas = 40.5 – 30.5 = 10. (selisih antara nilai terbesar dan terkecil batas kelas pada kelas ke-1)
Nilai tengah kelas: Nilai kelas merupakan nilai tengah dari kelas yang bersangkutan yang diperoleh dengan formula berikut: ½ (batas atas kelas+batas bawah kelas). Nilai ini yang dijadikan pewakil dari selang kelas tertentu untuk perhitungan analisis statistik selanjutnya. Contoh: Nilai kelas ke-1 adalah ½(31+40) = 35.5
Banyak kelas: Sudah jelas! Pada tabel ada 7 kelas.
Frekuensi kelas: Banyaknya kejadian (nilai) yang muncul pada selang kelas tertentu. Contoh, pada kelas ke-1, frekuensinya = 2. Nilai frekuensi = 2 karena pada selang antara 30.5 – 40.5, hanya ada 2 angka yang muncul, yaitu nilai ujian 31 dan 38.
Teknik pembuatan Tabel Distribusi Frekuensi (TDF)
Distribusi frekuensi dibuat dengan alasan berikut:- kumpulan data yang besar dapat diringkas
- kita dapat memperoleh beberapa gambaran mengenai karakteristik data, dan
- merupakan dasar dalam pembuatan grafik penting (seperti histogram).
Langkah-langkah dalam menyusun tabel distribusi frekuensi:
-
Urutkan data, biasanya diurutkan dari nilai yang paling kecil
-
Tujuannya agar range data diketahui dan mempermudah penghitungan frekuensi tiap kelas!
-
-
Tentukan range (rentang atau jangkauan)
-
Range = nilai maksimum – nilai minimum
-
-
Tentukan banyak kelas yang diinginkan. Jangan terlalu banyak/sedikit, berkisar antara 5 dan 20, tergantung dari banyak dan sebaran datanya.
-
Aturan Sturges:
-
Banyak kelas = 1 + 3.3 log n, dimana n = banyaknya data
-
-
Tentukan panjang/lebar kelas interval (p)
-
Panjang kelas (p) = [rentang]/[banyak kelas]
-
-
Tentukan nilai ujung bawah kelas interval pertama
Contoh:
Kita gunakan prosedur di atas untuk menyusun tabel distribusi frekuensi nilai ujian mahasiswa (Tabel 1).
Berikut adalah nilai ujian yang sudah diurutkan:
35 38 43 48 49 51 56 59 60 60
61 63 63 63 65 66 67 67 68 70
70 70 70 71 71 71 72 72 72 73
73 74 74 74 74 75 75 76 76 77
78 79 79 80 80 80 80 81 81 81
82 82 83 83 83 84 85 86 86 87
88 88 88 88 89 90 90 90 91 91
91 92 92 93 93 93 95 97 98 99
2. Range:
[nilai tertinggi – nilai terendah] = 99 – 35 = 64
3. Banyak Kelas:
Tentukan banyak kelas yang diinginkan.
Apabila kita lihat nilai Range = 64, mungkin banyak kelas
sekitar 6 atau 7.
Sebagai latihan, kita gunakan aturan Sturges.
banyak kelas = 1 + 3.3 x log(n)
= 1 + 3.3 x log(80)
= 7.28 ≈ 7
4. Panjang Kelas:
Panjang Kelas = [range]/[banyak kelas]
= 64/7
= 9.14 ≈ 10
(untuk memudahkan dalam penyusunan TDF)
5. Tentukan nilai batas bawah kelas pada kelas pertama.
Nilai ujian terkecil = 35
Penentuan nilai batas bawah kelas bebas saja,
asalkan nilai terkecil masih masuk ke dalam kelas tersebut.
Misalkan: apabila nilai batas bawah yang kita pilih adalah 26,
maka interval kelas pertama: 26 – 35, nilai 35 tepat jatuh
di batas atas kelas ke-1. Namun apabila kita pilih
nilai batas bawah kelas 20 atau 25, jelas nilai terkecil, 35,
tidak akan masuk ke dalam kelas tersebut.
Namun untuk kemudahan dalam penyusunan dan pembacaan TDF,
tentunya juga untuk keindahan, he2.. lebih baik kita memilih
batas bawah 30 atau 31. Ok, saya tertarik dengan angka 31,
sehingga batas bawahnya adalah 31.
Dari prosedur di atas, kita dapat info sebagai berikut:
Banyak kelas : 7
Panjang kelas : 10
Batas bawah kelas : 31
Selanjutnya kita susun TDF:
Form TDF:
------------------------------------------------------------
Kelas ke- | Nilai Ujian | Batas Kelas | Turus | Frekuensi
------------------------------------------------------------
1 31 -
2 41 -
3 51 -
: : -
6 81 -
7 91 -
------------------------------------------------------------
Jumlah
------------------------------------------------------------
Tabel berikut merupakan tabel yang sudah dilengkapi
| Kelas ke- | Nilai Ujian | Batas Kelas | Frekuensi (fi) |
| 1 | 31 – 40 | 30.5 – 40.5 | 2 |
| 2 | 41 – 50 | 40.5 – 50.5 | 3 |
| 3 | 51 – 60 | 50.5 – 60.5 | 5 |
| 4 | 61 – 70 | 60.5 – 70.5 | 13 |
| 5 | 71 – 80 | 70.5 – 80.5 | 24 |
| 6 | 81 – 90 | 80.5 – 90.5 | 21 |
| 7 | 91 – 100 | 90.5 – 100.5 | 12 |
| Jumlah | 80 |
atau dalam bentuk yang lebih ringkas:
| Kelas ke- | Nilai Ujian | Frekuensi (fi) |
| 1 | 31 – 40 | 2 |
| 2 | 41 – 50 | 3 |
| 3 | 51 – 60 | 5 |
| 4 | 61 – 70 | 13 |
| 5 | 71 – 80 | 24 |
| 6 | 81 – 90 | 21 |
| 7 | 91 – 100 | 12 |
| Jumlah | 80 |
Distribusi Frekuensi Relatif dan Kumulatif
Variasi penting dari distribusi frekuensi dasar adalah dengan menggunakan nilai frekuensi relatifnya, yang disusun dengan membagi frekuensi setiap kelas dengan total dari semua frekuensi (banyaknya data). Sebuah distribusi frekuensi relatif mencakup batas-batas kelas yang sama seperti TDF, tetapi frekuensi yang digunakan bukan frekuensi aktual melainkan frekuensi relatif. Frekuensi relatif kadang-kadang dinyatakan sebagai persen.Frekuensi relatif =
Contoh: frekuensi relatif kelas ke-1:
fi = 2; n = 80
Frekuensi relatif = 2/80 x 100% = 2.5%
| Kelas ke- | Nilai Ujian | Frekuensi relatif (%) |
| 1 | 31 – 40 | 2.50 |
| 2 | 41 – 50 | 3.75 |
| 3 | 51 – 60 | 6.25 |
| 4 | 61 – 70 | 16.25 |
| 5 | 71 – 80 | 30.00 |
| 6 | 81 – 90 | 26.25 |
| 7 | 91 – 100 | 15.00 |
| Jumlah | 100.00 |
Distribusi Frekuensi kumulatif
Variasi lain dari distribusi frekuensi standar adalah frekuensi kumulatif. Frekuensi kumulatif untuk suatu kelas adalah nilai frekuensi untuk kelas tersebut ditambah dengan jumlah frekuensi semua kelas sebelumnya.Perhatikan bahwa kolom frekuensi selain label headernya diganti dengan frekuensi kumulatif kurang dari, batas-batas kelas diganti dengan “kurang dari” ekspresi yang menggambarkan kisaran nilai-nilai baru.
| Nilai Ujian | Frekuensi kumulatif kurang dari |
| kurang dari 30.5 | 0 |
| kurang dari 40.5 | 2 |
| kurang dari 50.5 | 5 |
| kurang dari 60.5 | 10 |
| kurang dari 70.5 | 23 |
| kurang dari 80.5 | 47 |
| kurang dari 90.5 | 68 |
| kurang dari 100.5 | 80 |
| Nilai Ujian | Frekuensi kumulatif kurang dari |
| kurang dari 41 | 2 |
| kurang dari 51 | 5 |
| kurang dari 61 | 10 |
| kurang dari 71 | 23 |
| kurang dari 81 | 47 |
| kurang dari 91 | 68 |
| kurang dari 101 | 80 |
Histogram
Histogram adalah merupakan bagian dari grafik batang di mana skala horisontal mewakili nilai-nilai data kelas dan skala vertikal mewakili nilai frekuensinya. Tinggi batang sesuai dengan nilai frekuensinya, dan batang satu dengan lainnya saling berdempetan, tidak ada jarak/ gap diantara batang. Kita dapat membuat histogram setelah tabel distribusi frekuensi data pengamatan dibuat.
Poligon Frekuensi:
Poligon Frekuensi menggunakan segmen garis yang terhubung ke titik yang terletak tepat di atas nilai-nilai titik tengah kelas. Ketinggian dari titik-titik sesuai dengan frekuensi kelas, dan segmen garis diperluas ke kanan dan kiri sehingga grafik dimulai dan berakhir pada sumbu horisontal.
Ogive
Ogive adalah grafik garis yang menggambarkan frekuensi kumulatif, seperti daftar distribusi frekuensi kumulatif. Perhatikan bahwa batas-batas kelas dihubungkan oleh segmen garis yang dimulai dari batas bawah kelas pertama dan berakhir pada batas atas dari kelas terakhir. Ogive berguna untuk menentukan jumlah nilai di bawah nilai tertentu. Sebagai contoh, pada gambar berikut menunjukkan bahwa 68 mahasiswa mendapatkan nilai kurang dari 90.5.








Tidak ada komentar:
Posting Komentar