Sebelum ini sudah dijelaskan bagaimana dan kapan penggunaan uji t rata-rata sampel tunggal parametrik. kalau ada yang belum liat silahkan kesini Pengujian Rata-rata sampel tunggal (Single sample test of means) Parametrik. kali ini akan dicoba tutorial uji tersebut dengan menggunakan program R dengan paket R commander. berikut contoh kasus uji t rata-rata sampel tunggal:
Ujilah hipotesis bahwa isi kaleng rata – rata suatu jenis minyak pelumas adalah 10 liter. Bila random 10 kaleng adalah 10,2; 10; 9,7; 10,1; 9,8; 9,9; 10,4; 10,3; 9,8; dan 10,3 liter.Gunakan taraf nyata 1%!
Untuk melakukan pengujian rata-rata sampel tunggal seperti contoh kasus di atas pertama harus memasukkan data ke program R. untuk yang belum tau silahkan kesini Menambahkan/Input Data di Program R menggunakan paket R Commander, R-Commander menyediakan pilihan yaitu melalui menu Statistics, pilih Means, dan kemudian pilih single sample t- test sehingga diperoleh tampilan dialog isian untuk pengujian rata-rata sampel tunggal seperti pada Gambar di bawah Pada pilihan Peubah klik variabel dan kemudian isikan angka 10 pada kotak pilihan Hipotesis nol: mu=. Setelah itu, klik pilihan pada Hipotesis Alternatif sesuai dengan permasalahan diatas, yaitu Rerata populasi = mu0. Secara lengkap hipotesis statistik yang digunakan dalam pengujian rata-rata ini adalah sebagai berikut.

Kemudian tentukan Level Keyakinan pengujian yang akan digunakan, a = 1% tapi karena yang digunakan dua arah sehingga a = 0.5%. Hal ini berarti confidence level digunakan adalah 99.5%. Setelah semua isian dialog sudah sesuai dengan pengujian yang akan dilakukan, klik OK untuk menampilkan output dari pengujian ini.

Output hasil pengujian rata-rata sampel tunggal yang diperoleh dari contoh kasus di atas adalah sebagai berikut.
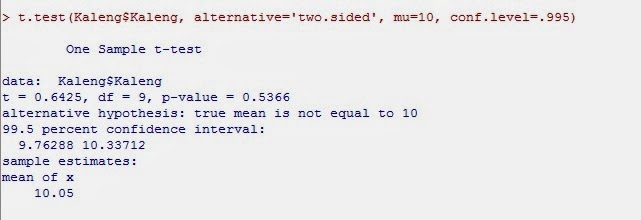
Hasil ini menunjukkan bahwa nilai statistik t yang diperoleh adalah 0.6425, dan nilai p-value pengujian adalah 0.5366. Dengan menggunakan kaidah pengambilan keputusan berdasarkan p-value, yaitu tolak H0 jika p-value lebih kecil dari nilai a, maka pada a=0.005 dapat disimpulkan bahwa pengujian menunjukkan gagal tolak H0. Dengan demikian dapat dijelaskan bahwa pernyatan rata-rata isi kaleng jenis pelumas 10 liter TIDAK BENAR.
Contoh kasus:
Ujilah hipotesis bahwa isi kaleng rata – rata suatu jenis minyak pelumas adalah 10 liter. Bila random 10 kaleng adalah 10,2; 10; 9,7; 10,1; 9,8; 9,9; 10,4; 10,3; 9,8; dan 10,3 liter.Gunakan taraf nyata 1%!
Untuk melakukan pengujian rata-rata sampel tunggal seperti contoh kasus di atas pertama harus memasukkan data ke program R. untuk yang belum tau silahkan kesini Menambahkan/Input Data di Program R menggunakan paket R Commander, R-Commander menyediakan pilihan yaitu melalui menu Statistics, pilih Means, dan kemudian pilih single sample t- test sehingga diperoleh tampilan dialog isian untuk pengujian rata-rata sampel tunggal seperti pada Gambar di bawah Pada pilihan Peubah klik variabel dan kemudian isikan angka 10 pada kotak pilihan Hipotesis nol: mu=. Setelah itu, klik pilihan pada Hipotesis Alternatif sesuai dengan permasalahan diatas, yaitu Rerata populasi = mu0. Secara lengkap hipotesis statistik yang digunakan dalam pengujian rata-rata ini adalah sebagai berikut.

Kemudian tentukan Level Keyakinan pengujian yang akan digunakan, a = 1% tapi karena yang digunakan dua arah sehingga a = 0.5%. Hal ini berarti confidence level digunakan adalah 99.5%. Setelah semua isian dialog sudah sesuai dengan pengujian yang akan dilakukan, klik OK untuk menampilkan output dari pengujian ini.

Output hasil pengujian rata-rata sampel tunggal yang diperoleh dari contoh kasus di atas adalah sebagai berikut.

Hasil ini menunjukkan bahwa nilai statistik t yang diperoleh adalah 0.6425, dan nilai p-value pengujian adalah 0.5366. Dengan menggunakan kaidah pengambilan keputusan berdasarkan p-value, yaitu tolak H0 jika p-value lebih kecil dari nilai a, maka pada a=0.005 dapat disimpulkan bahwa pengujian menunjukkan gagal tolak H0. Dengan demikian dapat dijelaskan bahwa pernyatan rata-rata isi kaleng jenis pelumas 10 liter TIDAK BENAR.
Kalau ada kritik, saran dan pertanyaan silahkan komentarnya di kolom komentar di bawah. Kalau tidak punya akun silahkan ditulis sebelah kiri yaitu kolom “Chatbox”. Mohon dicantumkan email atau contact yang bisa dihubungi.
Sumber: Buku(Suhartono, 2008):Analisis Data statistik dengan R









Tidak ada komentar:
Posting Komentar