[TUTORIAL] contoh kasus analisis faktor dengan SPSS

contoh kasus untuk analisis faktor

Berdasarkan SDKI 2002-2003 cakupan imunisasi lengkap anak usia 12-23 bulan di Indonesia berdasarkan informasi dari KMS (Kartu Menuju Sehat) atau laporan ibu sebesar 52 persen. Angka ini masih keci bilBerdasarkan SDKI 2002-2003 cakupan imunisasi lengkap anak usia 12-23 bulan di Indonesia berdasarkan informasi dari KMS (Kartu Menuju Sehat) atau laporan ibu sebesar 52 persen. Angka ini masih keci bila dibandingkan dengan 80 persen angka cakupan imunisasi lengkap yang ditargetkan oleh UCI ( Universal Chilhood Imunization). Bila dilihat pada cakupan imunisasi lengkap pada tingkat propinsi hanya ada dua propinsi yang telah memenuhi target UCI yaitu Yogyakarta (84 persen) dan Bali (80 persen). Oleh karena itu, ingin diketahui faktor dominan apakah yang mempengaruhi ketidaklengkapan imunisasi anak usia 12-23 bulan di Indonesia. Faktor dominan yang ingin diketahui pengaruhnya dibatasi pada karakteristik ibu dan ayah.

Sehingga inti dalam kasus ini yaitu ingin melihat Faktor – Faktor yang Mempengaruhi ketidaklengkapan Imunisasi Anak Usia 12 – 23 Bulan di Indonesia Tahun 2003. Data yang digunakan dalam kasus di atas berasal dari Survei Demografi dan Kesehetan Indonesia, 2002-2003. Silahkan lihat kalau coba-coba disini. data imunisasi

Langkah-langkah dalam Analisis faktor dengan SPSS

Menyamakan satuan data

1. Buka data yang sudah dimasukkan. Tampilannya seperti berikut.
   
2. Karena data memiliki variasi yang besar (karena satuan dan rentang data yang berbeda-beda), maka distandardisasi terlebih dahulu dengan mentransformasikan ke dalam bentuk Z-score, yaitu dengan klik Descriptive Statistics→Descriptives. Maka akan muncul tampilan berikut.
   
3. Pada kolom Variable(s) masukkan semua variabel, lalu centang pilihan ‘Save standardized values as variables’. Kemudian Pilih Menu Options maka akan muncul tampilan berikut.
   
4. Beri tanda cek pada Mean, dengan pada Dispersion dicek Standard Deviation dan Variance, serta beri tanda cek pada Variable List pada Display Order. kemudian Klik Continue. Maka akan muncul variabel baru seperti berikut.
   

Melakukan Analisis Faktor

1. Pilih Analyze >> Data Reduction >> Factor. Maka akan muncul jendela Factor Analysis
   
2. Pilih semua variabel sebagai variabel analisis. Klik Descriptive, pada bagian Correlation Matrix beri tanda cek pada Coefficient,significan levels,  invers, Anti image dan KMO and Bartlett’s test of sphericity. Klik Continue.
   
3. Kemudian klik pada Extraction dan pastikan pilihan Analyze pada correlation matrix dan pada bagian Display beri tanda cek pada kedua pilihan. Sebagai kriteria ekstaksi (Extraction) kita akan menggunakan eigenvalue, yaitu Eigenvalues over: 1. Klik Continue.
   
4. Klik Rotation lalu pilih Varimax dan pada Display pilih Rotated Solution. Klik Continue
   
5. Klik Scores, lalu beri tanda cek Save as Variables dengan Method: Regression dan Display factor score coefficient matrix, agar kita bisa melihat nilai variabel/faktor baru yang terbentuk. Klik Continue.
   
6. Setelah itu klik OK, akan muncul kumpulan output yang siap diinterpretasi.

Intrepretasi

Deskripsi

Deskripsi Data

Correlation Matrix

Tabel Correlation Matrix merupakan tabel matriks korelasi yang berisi nilai-nilai korelasi antara variabel-variabel yang akan dianalisis. Pada bagian Correlation dapat dilihat besarnya korelasi antarvariabel. Sebagai contoh, korelasi antara variabel ibu tinggal di desa dengan ibu yang bekerja sebesar -0,573 yang menunjukkan terdapat hubungan yang cukup kuat dan negative. Artinya, semakin banyak persentase ibu yang tinggal di desa, maka makin sedikit persentase ibu yang bekerja.

Kemudian pada baris sig.(1-tailed) menunjukkan signifikansi korelasi antara variabel-variabel tersebut. Korelasi antara variabel ibu tinggal di desa dengan ibu yang bekerja signifikan, terlihat dari nilai p-value sebesar 0,001(<0.05) yang berarti terdapat memang terdapat hubungan antara variabel ibu tinggal di desa dengan variabel ibu yang bekerja.

Inverse of Correlation Matrix

Sedangkan table Inverse of Correlation Matrix menyatakan nilai-nilai pada matriks korelasi setelah matriks tersebut diinverskan.

Catatan : Dalam kasus ini, digunakan matriks korelasi untuk keperluan analisis faktor sebab data yang digunakan memiliki satuan yang berbeda-beda,sehingga distandarisasi menggunakan matriks korelasi untuk menghilangkan bias.

Analisis Inferensia

KMO dan Bartlett’s Test

Berdasarkan Bartlett’s Tes of Sphericity dengan Chi-Square 94,304 (df 45) dan nilai sig = 0,000 < 0,05 menunjukkan bahwa matriks korelasi bukan merupakan matriks identitas sehingga dapat dilakukan analisis komponen utama. Di samping itu, Nilai KMO yang dihasilkan adalah sebesar 0.574 serta p-value sebesar 0,000 (<0,05) , nilai tersebut jatuh dalam kategori “lebih dari cukup” layak untuk kepentingan analisis faktor. Oleh karena itu, variabel – variabel dapat dianalisis lebih lanjut (AA Afifi,1990:Dillon dan Goldstein,1984).

Tabel Anti-Image Matrices

Selain pengecekan terhadap KMO and Bartlett test, dilakukan juga pengecekan Anti Image matrices untuk mengetahui apakah variabel – variabel secara parsial layak untuk dianalisis dan tidak dikeluarkan dalam pengujian. Berdasarkan tabel di atas, terlihat bahwa dari sepuluh variabel yang akan dianalisis, terdapat dua variabel yang memiliki nilai MSA (dapat dilihat pada output yang bertanda a pada kolom Anti-Image Correlation) < 0,5 yaitu variabel ibu tidak bekerja dan variabel bapak yang tidak bekerja. Karena ada variabel yang nilai MSA nya < 0,5 , maka variabel tersebut tidak dapat dianalisis lebih lanjut. Meskipun ada dua variabel yang nilai MSA nya < 0,5, namun kita tidak harus membuang dua variabel sekaligu. Pilih salah satu variabel yang memiliki MSA terkecil, yaitu bapak tidak bekerja sebesar 0,360 sehingga variabel tersebut dikeluarkan dan dilakukan pengujian ulang terhadap kesembilan variabel lainnya seperti pada cara di atas.

Setelah variabel bapak tidak bekerja dikeluarkan, maka nilai KMO meningkat menjadi 0,652 dan tingkat signifikansi 0,000.Pengurangan variabel yang “tidak layak” meningkatkan nilai KMO sehingga cukup beralasan untuk melakukan pengurangan tersebut Hal ini dapat menunjukkan bahwa kesembilan variabel tersebut’ lebih dari cukup’ layak untuk dilakukan analisis faktor.

Communalities

Dari keseluruhan nilai dalam table communalities, diperoleh bahwa kesembilan variabel awal mempunyai nilai communalities yang besar ( > 0.5). Hal ini dapat diartikan bahwa keseluruhan variabel yang digunakan memiliki hubungan yang kuat dengan faktor yang terbentuk. Dengan kata lain, semakin besar nilai dari communalities maka semakin baik analisis faktor, karena semakin besar karakteristik variabel asal yang dapat diwakili oleh faktor yang terbentuk.

1. Keeratan hubungan variabel ibu bekerja terhadap faktor yang terbentuk sebesar 0,811 artinya hubungan variabel ibu bekerja terhadap faktor yang terbentuk erat. Atau dapat juga dikatakan kontribusi variabel ibu bekerja terhadap faktor yang terbentuk sebesar 81,1 %.
2. Kemudian, keeratan hubungan variabel bapak yang pendidikannya SD ke bawah sebesar 0,849 artinya hubungan variabel bapak yang pendidikannya SD ke bawah terhadap faktor yang terbentuk erat. Atau dapat juga dikatakan kontribusi variabel variabel bapak yang pendidikannya SD ke bawah terhadap faktor yang terbentuk sebesar 84,9 %.

Total Variance Explained

Table Total Variance Explained menunjukkan besarnya persentase keragaman total yang mampu diterangkan oleh keragaman faktor - faktor yang terbentuk. Dalam tabel tersebut juga terdapat nilai eigenvalue dari tiap-tiap faktor yang terbentuk. Faktor 1 memiliki eigenvalue sebesar 2,991, Faktor 2 sebesar 2,120, dan Faktor 3 sebesar 1,323. Untuk menentukan berapa komponen/faktor yang dipakai agar dapat menjelaskan keragaman total maka dilihat dari besar nilai eigenvaluenya, komponen dengan eigenvalue >1 adalah komponen yang dipakai. Kolom ‘cumulative %’ menunjukkan persentase kumulatif varians yang dapat dijelaskan oleh faktor. Besarnya keragaman yang mampu diterangkan oleh Faktor 1 sebesar 33,233 persen, sedangkan keragaman yang mampu dijelaskan oleh Faktor 1 dan 2 sebesar 56,787 persen. Ketiga faktor mampu menjelaskan keragaman total sebesar 71,485 persen. Berdasarkan alasan nilai eigen value ketiga faktor yang lebih dari 1 dan besarnya persentase kumulatif ketiga faktor sebesar 71,485 persen, dapat disimpulkan bahwa ketiga faktor sudah cukup mewakili keragaman variabel – variabel asal.

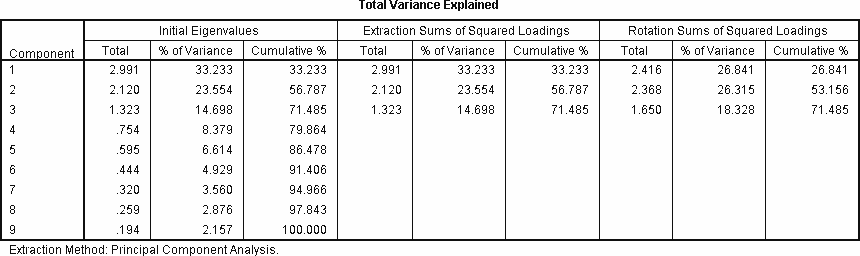
Proporsi keragaman data yang dijelaskan tiap komponen setelah dilakukan rotasi terlihat lebih merata daripada sebelum dilakukan rotasi. Faktor pertama menerangkan keragaman data dengan proporsi terbesar, yaitu 33,233 persen menurut metode ekstraksi dengan analisis faktor (sebelum rotasi) dan dengan analisis faktor (setelah rotasi) keragaman data awal dapat dijelaskan sebesar 26,841 persen. Kemudian untuk faktor kedua menerangkan keragaman data awal dengan proporsi 23,554 persen menurut metode ekstraksi dengan analisis faktor (sebelum rotasi) dan dengan analisis faktor (setelah rotasi) keragaman data awal dapat dijelaskan sebesar 26,315 persen. Sedangkan untuk faktor ketiga menerangkan keragaman sebesar 14,698 persen sebelum dilakukan rotasi dan naik menjadi 18,328 persen setelah dirotasi.

Proporsi keragaman data yang lebih merata setelah dilakukan rotasi menunjukkan keseragaman data awal yang dijelaskan oleh masing-masing faktor menjadi maksimum.

Scree Plot

Scree Plot adalah salah satu alternatif yang dapat digunakan untuk membantu peneliti menentukan berapa banyak faktor terbentuk yang dapat mewakili keragaman peubah – peubah asal. Bila kurva masih curam, akan nada petunjuk untuh menambahkan komponen. Bila kurva sudah landai, akan ada petunjuk untuk menghentikan penambahan komponen, walaupun penilaian curam/landai bersifat subjektif peneliti. Dari scree plot di atas, terlihat pada saat satu komponen terbentuk, kurva masih menunjukkan kecuraman, begitu juga pada saat di titik ke-2, garis kurva masih tajam, di titik ke-3 garis kurva masih tajam namun sedikit berbeda dari pola kedua garis sebelumnya. Setelah melewati titik ke-3, garis kurva sudah mulai landai, semakin ke kanan akan semakin landai. Dari penjelasan di atas, dapat kita tarik kesimpulan bahwa terdapat tiga komponen atau faktor yang terbentuk.

Table component matrix 

Table component matrix menunjukkan besarnya korelasi tiap variabel dalam faktor yang terbentuk. Nilai – nilai koefisien korelasi antara variabel dengan faktor - faktor yang terbentuk (loading factor) dapat dilihat pada table Component Matrix. Ketiga faktor tersebut menghasilkan matrik loading faktor yang nilai-nilainya merupakan koefisien korelasi antara variabel dengan faktor-faktor tersebut. Bila dilihat variabel –variabel yang berkorelasi terhadap setiap faktornya, ternyata loading faktor yang dihasilkan belum mampu memberikan arti sebagaimana yang diharapkan. Hal ini terlihat dari variabel ibu yang tidak punya KMS dimana korelasi variabel ini dengan faktor 1 sebesar 0,609, sedangkan dengan faktor 2 sebesar -0,508 (tanda negative hanya menunjukkan arah korelasi), sehingga kita sulit untuk memutuskan apakah variabel ibu tidak punya KMS dimasukkan ke faktor 1 atau faktor 2. Tiap faktor belum dapat diinterpretasikan dengan jelas sehingga perlu dilakukan rotasi dengan metode varimax. Rotasi varimax adalah rotasi orthogonal yang membuat jumlah varian faktor loading dalam masing-masing faktor akan menjadi maksimum, dimana nantinya peubah asal hanya akan mempunyai korelasi yang tinggi dan kuat dengan faktor tertentu saja (korelasinya mendekati 1) dan tentunya memiliki korelasi yang lemah dengan faktor yang lainnya (korelasinya mendekati 0). Hal yang demikian belum tercapai pada table component matrix diatas.

Rotated Component Matrix

Setelah dilakukan rotasi faktor dengan metode varimax, diperoleh table seperti yang tertera di atas yaitu Rotated Component Matrix. Terdapat perbedaan nilai korelasi variabel dengan setiap faktor sebelum dan sesudah dilakukan rotasi varimax. Terlihat bahwa loading faktor yang dirotasi telah memberikan arti sebagaimana yang diharapkan dan setiap faktor sudah dapat diinterpretasikan dengan jelas. Terlihat pula bahwa setiap variabel hanya berkorelasi kuat dengan salah satu faktor saja (tidak ada variabel yang korelasinya < 0,5 di ketiga faktor). Dengan demikian, lebih tepat digunakan loading faktor yang telah dirotasi sebab setiap faktor sudah dapat menjelaskan keragaman variabel awal dengan tepat dan hasilnya adalah sebagai berikut

1. Faktor 1 , beberapa variabel yang memiliki korelasi yang kuat dengan faktor 1 , yaitu variabel ibu yang tinggal di desa, ibu yang mengakses koran, ibu yang bekerja dan urutan anak.
2. Faktor 2, terdapat beberapa variabel yang memiliki korelasi yang kuat dengan faktor 2 , yaitu variabel ibu yang mengakses radio, ibu yang mengakses TV, ibu yang tidak punya KMS, dan bapak yang pendidikannya SD ke bawah.
3. Faktor 3, dalam faktor ini tiga variabel yang memiliki korelasi yang kuat dengan faktor 3, yaitu variabel ibu yang pendidikannya SD ke bawah.

Component Transformation Matrix

Tabel Component Transformation Matrix berfungsi untuk menunjukkan apakah faktor – faktor yang terbentuk sudah tidak memiliki korelasi lagi satu sama lain atau orthogonal. Bila dilihat dari table Component Transformation Matrix, nilai – nilai korelasi yang terdapat pada diagonal utama berada di atas 0,5 yaitu -0,606;0,614;0,891. Hal ini menunjukkan bahwa ketiga faktor yang terbentuk sudah tepat karena memiliki korelasi yang tinggi pada diagonal – diagonal utamanya.

Untuk lengkapnya bisa didownload disini beserta intrepretasi ouputnya Tutorial contoh analisis faktor beserta hasil intrepretasi dengan SPSS

Untuk sedikit materi analisis faktor bisa dilihat disini gan. teori analisis faktor